Evaluation of Prediction Equations for Confined Circular Concrete Members of Core Concrete Compressive Strength

Ho-Young Kim; Jae-Hoon Lee

doi:10.22725/JSRP.2024.2.1.30

Preview

Research Article

Journal of Structure Research and Practice. 30 June 2024. 30-38
https://doi.org/10.22725/JSRP.2024.2.1.30

Evaluation of Prediction Equations for Confined Circular Concrete Members of Core Concrete Compressive Strength

횡구속된 원형 콘크리트 부재의 심부 콘크리트 압축강도 예측식 평가

Ho-Young Kim¹^*

Jae-Hoon Lee²

김 호영¹^*

이 재훈²

¹Manager, Structure Department, Yooshin, Seoul 06252, Korea

²Professor, Department of Civil Engineering, Yeungnam University, Gyeongsan 38541, Korea

¹유신 구조부 과장

²영남대학교 건설시스템공학과 교수

^{*Corresponding Author}

License (open-access, http://creativecommons.org/licenses/by-nc/4.0/):

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

Confining effect is one of the important items for seismic design and performance evaluation of reinforced concrete structures, since the concrete confined by transverse reinforcement shows high load resistance capacity and ductility. In this study, the accuracy of the 12 proposed equations were evaluated by comparing the test results of 189 transversely confined circular sections. As a result, the equations of proposed by Desayi et al., by El-Dash and Ahmad, by Sun and Sakino, by Eurocode 2, and by Korean KDS design codes provided relatively low variability and the equation of the Korean Design Standard showed the smallest coefficient of variation and predicted the relatively accurate results compared to the test data.

Keywords

transverse steel

confining effect

circular section

strength of confined concrete

Korean Design Standard

횡방향철근으로 구속된 콘크리트는 높은 하중저항성능과 연성능력을 발휘하므로, 횡구속효과는 철근콘크리트 구조물의 내진설계와 성능평가에 적용되는 중요한 항목 중이다. 이 연구에서는 지금까지 제안된 모델을 대상으로 189개의 횡구속된 원형단면의 압축강도 실험결과를 비교하여 제안식 12개에 대한 정확성을 평가하였다. 그 결과 Desayi 등, El-Dash와 Ahmad, Sun과 Sakino, Eurocode 2, 한국 KDS 설계기준의 수식은 비교적 변동성이 적었고, 한국 설계기준의 수식이 가장 작은 값의 변동계수를 보이며 실험값을 비교적 정확하게 예측하는 것으로 나타났다.

키워드

횡방향철근

횡구속효과

원형단면

횡구속된 콘크리트 압축강도

한국 설계기준

MAIN

1. 서 론
2. 횡구속된 콘크리트의 압축강도 산정 수식
3. 횡구속된 콘크리트 압축강도 산정 수식의 평가
4. KDS 14 20 20 콘크리트구조 휨 및 압축 설계기준의 나선철근비
5. 결 론

1. 서 론

Fig. 1(a)와 같이 횡방향철근으로 구속된 콘크리트는 높은 하중저항성능과 연성능력을 발휘하므로, 횡구속효과는 철근콘크리트 구조물의 내진설계와 성능평가에 적용되는 중요한 항목 중 하나이다. 횡구속효과에 대한 첫 번째 연구(Richart et al. 1928)가 발표된 후 1900년대 후반부터 많은 연구자들이 횡방향철근으로 구속된 콘크리트의 압축강도를 예측하는 수식을 제안하였다. 설계기준 중에서는 Eurocode 2(2004)와 한국의 KDS 24 14 21 콘크리트교 설계기준(KIBSE 2021) 및 KDS 14 20 20 콘크리트구조 휨 및 압축 설계기준(KCI 2022)이 Fig. 1(b)와 같은 횡구속된 콘크리트의 압축응력-변형률 곡선을 규정하고 있다. 이 연구에서는 189개의 횡구속된 원형단면의 압축강도 실험결과와 비교하여 지금까지 제안된 횡구속된 콘크리트의 압축강도 산정 수식들의 정확성을 평가하고자 한다.

https://cdn.apub.kr/journalsite/sites/kibse/2024-002-01/N0510020104/images/kibse_02_01_04_F1.jpg

Fig. 1

Confining effect by transverse reinforcement

2. 횡구속된 콘크리트의 압축강도 산정 수식

횡구속된 콘크리트의 압축강도를 산정하는 수식은 횡방향으로 유압을 가한 3축 압축실험 결과를 바탕으로 Richart et al.(1928)이 처음 제안하였다. Table 1에 나타낸 바와 같이 Richart et al.의 제안식은 비횡구속 콘크리트의 압축강도 $f_{c k}$ 에 횡방향 구속응력 $f_{l}$ 의 4.1배가 증가된 값으로 계산된다. 그 후 1900년대 후반부터 많은 연구자들이 횡방향철근에 의한 구속응력을 결정하는 방법과 그 영향을 반영하여 횡방향철근의 항복강도 $f_{y h}$ 가 포함된 수식을 제안하였고, 모델코드인 fib Model Code와 실행코드인 Eurocode 2와 KDS 24 14 21 콘크리트교 설계기준 및 KDS 14 20 20 콘크리트구조 휨 및 압축 설계기준에서 횡구속된 콘크리트의 압축응력-변형률 곡선을 규정하고 있다. Table 1은 여러 연구자들이 제안한 횡구속된 콘크리트의 압축강도 산정 수식과 설계기준에서 규정하고 있는 수식을 나타낸 것이다. 여기서, $ρ_{s}$ 는 횡방향철근과 심부콘크리트의 체적비, $d_{s p}$ 는 횡방향철근 지름, $s$ 는 횡방향철근 수직간격, $d_{c}$ 는 심부콘크리트의 지름이다.

Table 1.

Proposed equations of confined concrete compression strength

	Proposed Equation
Richart et al. (1928)	$f_{c k, c} = f_{c k} + 4.1 f_{l}$
Desayi et al. (1978)	$f_{c k, c} = f_{c k} (1 + 2.3 C_{i}), C_{i} = (ρ_{s} - ρ_{s}) \frac{f_{y h}}{f_{c k}}, ρ_{s} = \frac{4 A_{s p}}{d_{c} s}$
Ahmad and Shah (1982)	$f_{c k, c} = f_{c k} + k_{1} {(f_{r})}_{p}, {(f_{r})}_{p} = \frac{ρ_{s} f_{y h}}{2} (1 - \sqrt{\frac{s}{1.25 d_{c}}}), k_{1} = \frac{6.61}{\sqrt{f_{c k}}} {(f_{r})}_{p}^{0.04}$
Scott et al. (1982)	$f_{c k, c} = K f_{c k}, K = 1 + \frac{ρ_{s} f_{y h}}{f_{c k}}$
Mander et al. (1988a)	$f_{c k, c} = f_{c k} (2.254 \sqrt{1 + \frac{7.94 f_{l}}{f_{c k}}} - 2 \frac{f_{l}}{f_{c k}} - 1.254), f_{l} = \frac{1}{2} ρ_{s} k_{e} f_{y h}, k_{e} = \frac{A_{e}}{A_{c} (1 - ρ_{c c})}$ $A_{e} = (1 - \sum \frac{w^{2}}{6 b_{c} d_{c}}) (1 - \frac{s}{2 b_{c}}) (1 - \frac{s}{2 d_{c}})$
El-Dash and Ahmad (1995)	$f_{c k, c} = f_{c k} + k_{l} {(f_{r})}_{p}, {(f_{r})}_{p} = \frac{ρ_{s} f_{y h}}{2} (1 - \sqrt{\frac{s}{1.25 d_{c}}}), k_{1} = 5.1 {(\frac{f_{c k}}{f_{y h}})}^{0.5} {(\frac{d_{s p}}{ρ_{s}})}^{0.25}$
Razvi and Saacioglu (1999a)	$f_{c k, c} = f_{c k} + k_{1} f_{l}, f_{l} = \frac{2 A_{s p} f_{y h}}{d_{c} s}, k_{1} = 6.4 {(f_{l})}^{- 0.17}$
Sun and Sakino (2000)	$f_{c k, c} = f_{c k} (1 + 4.1 \frac{0.5 ρ_{s} f_{y h}}{f_{c k}}) {(1 - \frac{s}{2 d_{c}})}^{2}$
Bing et al. (2001)	$f_{c k, c} = f_{c k} (2.254 \sqrt{1 + \frac{7.94 α_{s} f_{l}}{f_{c k}}} - \frac{2 α_{s} f_{l}}{f_{c k}} - 1.254)$ $α_{s} = (21.2 - 0.35 f_{c k}) \frac{f_{l}}{f_{c k}}, f_{c k} \leq 52 M P a, α_{s} = 3.1 \frac{f_{l}}{f_{c k}}, f_{c k} > 52 M P a$
Moon (2010)	$f_{c k, c} = f_{c k} + 3 f_{r}, f_{r} = \frac{1}{2} ρ_{s} f_{y h} {(1 - \frac{1}{2 d_{c}})}^{2} 0.73$
fib Model Code 2010	$f_{c k, c} = f_{c k} (1 + 3.5 {(\frac{σ_{2}}{f_{c k}})}^{\frac{3}{4}}), w_{c} = \frac{A_{s c} f_{y d}}{s d_{c} f_{c d}}$ $σ_{2} = w_{c} f_{c d} {(1 - \frac{s}{d_{c}})}^{2}$ , for hoop reinforcement $σ_{2} = w_{c} f_{c d} (1 - \frac{s}{d_{c}})$ , for spiral reinforcement
Eurocode 2	$f_{c k, c} = f_{c k} (0.1 + 5.0 σ_{2} / f_{c k}), σ_{2} \leq 0.05 f_{c k}, f_{c k, c} = f_{c k} (0.1 + 2.5 σ_{2} / f_{c k}), σ_{2} > 0.05 f_{c k}$
KDS 14 20 20 KDS 24 14 21	$f_{c k, c} = f_{c k} + 3.7 f_{2}, f_{2} = \frac{1}{2} ρ_{s} f_{y h} (1 - \frac{s}{d_{c}}) = \frac{2 A_{s p} f_{y h}}{s d_{c}} (1 - \frac{s}{d_{c}})$

3. 횡구속된 콘크리트 압축강도 산정 수식의 평가

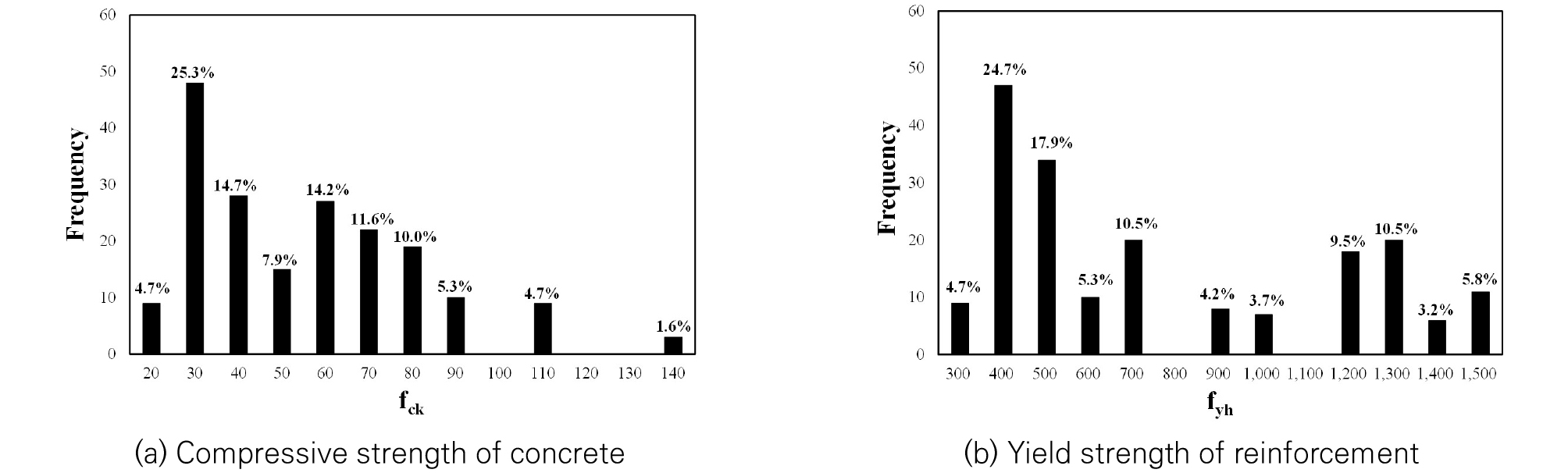
이 연구에서는 Table 1에 소개된 연구자들과 Mander et al.(1988b); Sakino(1993); Issa and Tobaa(1994); Razvi and Saatcioglu(1999b); Kim et al.(2012); Yoo(2010); Assa et al.(2001); Martinez(1983)들이 수행한 횡방향철근으로 구속된 콘크리트 부재의 실험결과 189개를 취합하여 분석하였다. 각 문헌에서의 실험자료 중 횡방향철근이 없거나 횡방향철근이 번들로 배치된 실험자료, 경량골재 콘크리트가 적용된 실험자료, 문헌에서 표기가 불명확한 실험자료 등은 분석에서 제외시켰다. 각 연구자들의 실험결과에 적용된 재료강도 분포는 Fig. 2와 같다. Fig. 2(a)와 같이 콘크리트 압축강도는 약 25%로 20~30 MPa이 가장 많으며 다음으로 30~40 MPa이 약 15%, 50~60 MPa가 약 14%로 많이 분포하였다. 철근의 항복강도는 Fig. 2(b)와 같이 300~400 MPa가 약 25%로 가장 많고 다음으로 400~500 MPa가 약 18%로 많이 분포하였다. 이러한 재료강도의 분포로 봤을 때, 189개의 실험자료는 현재 실무에서 많이 적용되는 재료강도와 유사한 것을 알 수 있다.

https://cdn.apub.kr/journalsite/sites/kibse/2024-002-01/N0510020104/images/kibse_02_01_04_F2.jpg

Fig. 2

Distribution of material strength

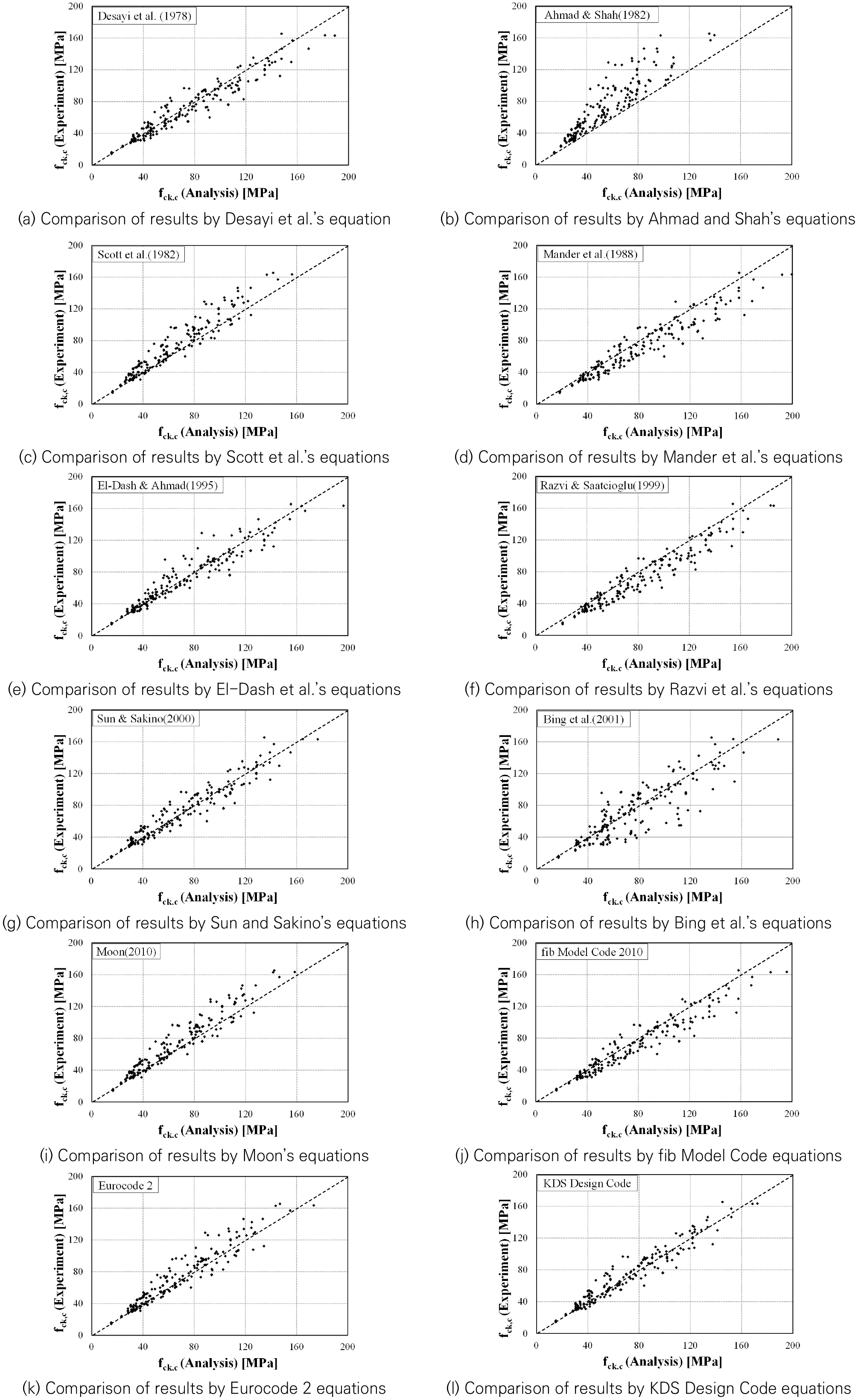
Fig. 3은 Table 1에 소개된 연구자들이 수행한 횡방향철근으로 구속된 콘크리트 부재의 실험결과 189개에 대하여 각 산정 수식의 계산결과를 비교한 것이다. Fig. 3의 (b), (c), (i)에 나타난 바 와 같이 Ahmad and Shah, Scott et al., Moon의 수식은 전반적으로 실험값보다 작은 값을 보이며, Fig. 3의 (d), (f), (j)와 같이 Mander et al., Razvi and Saacioglu, fib Model Code의 수식은 전반적으로 실험값보다 큰 값을 보인다. 여기서 fib Model Code의 수식에는 콘크리트에 1.5, 철근에 1.15의 재료부분안전계수를 적용하였다. 한편 Fig. 3(h)와 같이 Bing et al.(2001)의 수식은 실험결과 값과 비교하여 중심선으로 부터 분포가 넓게 분포되는 결과를 보이며, Fig. 2의 (a), (e), (g), (k), (l)과 같이 Desayi et al., El-Dash and Ahmad, Sun and Sakino, Eurocode 2, KDS 설계기준의 수식은 실험결과와 비교하여 비교적 중심선에 가깝게 분포되는 결과를 보인다. 여기서, Eurocode 2에는 횡방향철근에 의한 구속응력 $σ_{2}$ 의 결정방법이 규정되어 있지 않으므로, Eurocode 2의 모태가 되는 fib Model Code에 따라 $σ_{2}$ 를 계산하였다.

https://cdn.apub.kr/journalsite/sites/kibse/2024-002-01/N0510020104/images/kibse_02_01_04_F3.jpg

Fig. 3

Comparison of confined concrete compressive strength and predicted values

Table 2.

Maximum, minimum, average, standard deviation and coefficient of variation of test/equation ratio

Model		Maximum	Minimum	Average	Standard Deviation	Coefficient of Variation
Desayi et al. (1978)		1.384	0.655	0.968	0.139	0.144
Ahmad and Shah (1982)		2.271	0.971	1.315	0.248	0.189
Scott et al. (1982)		1.566	0.813	1.124	0.157	0.139
Mander et al. (1988)		1.229	0.601	0.886	0.126	0.143
El-Dash and Ahmad (1995)		1.670	0.704	1.009	0.145	0.144
Razvi and Saacioglu (1999)		1.206	0.586	0.870	0.122	0.141
Sun and Sakino (2000)		1.401	0.667	1.022	0.150	0.147
Bing et al. (2001)		1.889	0.487	0.944	0.233	0.247
Moon (2010)		1.539	0.796	1.103	0.150	0.136
fib Model Code 2010	by $f_{c d}$ & $f_{y d}$	1.281	0.634	0.923	0.126	0.136
fib Model Code 2010	by $f_{c k}$ & $f_{y h}$	1.254	0.604	0.890	0.124	0.140
Eurocode2		1.439	0.748	1.039	0.139	0.134
KDS 14 20 20 KDS 24 14 21		1.439	0.748	1.028	0.136	0.132

Table 2는 Fig. 3에 나타낸 결과를 정량적으로 비교하기 위한 것으로, 실험값을 수식의 값으로 나눈 비율의 최댓값(maximum), 최솟값(minimum), 평균값(average), 표준편차(standard deviation), 변동계수(coefficient of variation)를 나타낸 것이다. Table 2에 나타낸 바와 같이 El-Dash and Ahmad의 수식은 평균값이 1.009로 1.0에 가장 가깝지만, 0.145의 표준편차와 0.144의 변동계수가 Eurocode 2나 KDS 설계기준의 수식보다 크다. Razvi and Saatcioglu의 수식은 표준편차가 0.122로 가장 작지만, 평균값이 0.870으로 1.0과 큰 차이를 보인다. KDS 설계기준의 수식은 변동계수가 0.132로 모든 수식 중 가장 작은 값을 보이며, 평균값이 1.028이고 표준편차가 0.136으로 실험값을 비교적 정확하게 예측하는 것으로 나타났다. Eurocode 2의 수식은 평균값 1.039, 표준편차 0.139, 변동계수 0.134로 KDS 설계기준의 수식보다 다소 높은 값을 보였다. Table 2에서 fib Model Code의 수식을 적용한 결과는 콘크리트에 1.5의 재료부분안전계수를 적용한 $f_{c d}$ 와 철근에 1.15의 재료부분안전계수를 적용한 $f_{y d}$ 로 계산한 경우와 재료부분안전계수를 적용하지 않은 $f_{c k}$ 와 $f_{y h}$ 로 계산한 경우인데, 두 가지 결과에 큰 차이는 보이지 않았으나 $f_{c d}$ 와 $f_{y d}$ 로 계산한 경우에 평균값이 1.0에 더 근접하였다.

한편, 횡구속된 콘크리트의 압축강도 $f_{c k, c}$ 와 비횡구속 콘크리트의 압축강도 $f_{c k}$ 의 관계는 횡방향 구속응력 $f_{2}$ 에 곱하여지는 계수 $k_{m}$ 을 이용하여 다음과 같이 식 (1) ~ 식 (3)으로 나타낼 수 있다.

(1)

f_{c k, c} = f_{c k} + k_{m} f_{2}

(2)

\frac{f_{c k, c}}{f_{c k}} = 1 + k_{m} \frac{f_{2}}{f_{c k}}

(3)

\frac{f_{c k, c}}{f_{c k}} - 1 = k_{m} \frac{f_{2}}{f_{c k}}

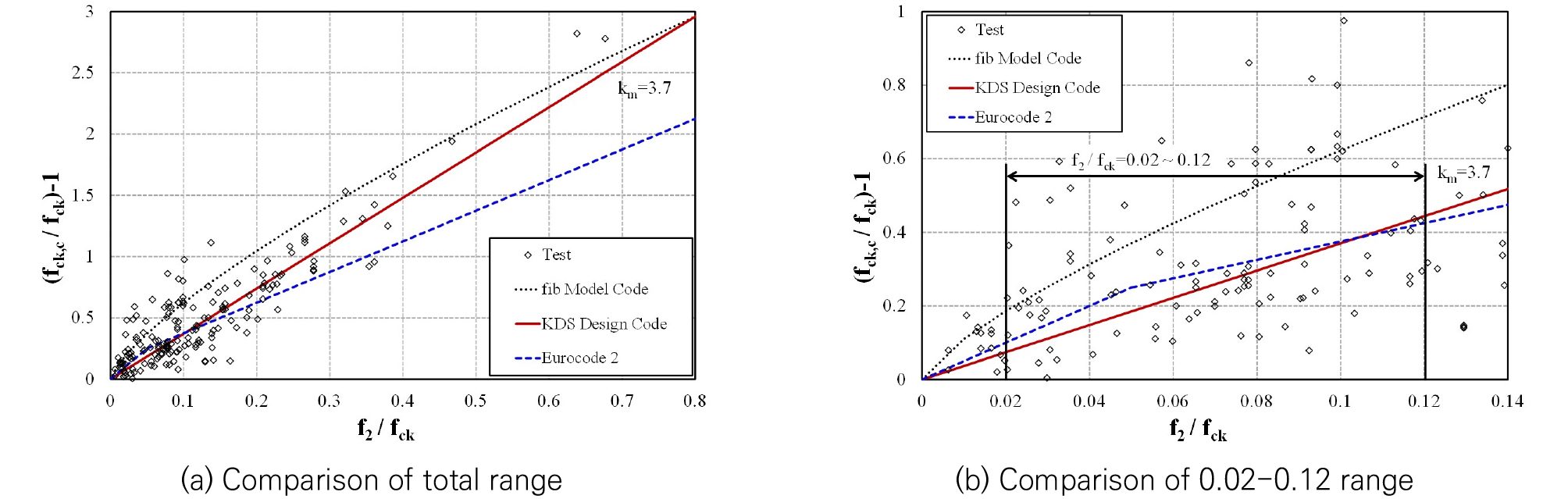
Fig. 4는 실험값에 대하여 fib Model Code, Eurocode 2, KDS 설계기준의 $k_{m}$ 값을 비교한 것이다. 여기서 Fig. 4(a)는 189개 실험값 모두를 나타낸 것이며, 실제 구조물에는 $f_{2} / f_{c k}$ 값으로 주로 0.02~0.12가 적용된다고 생각되므로 Fig. 4(b)는 $f_{2} / f_{c k}$ 가 0.14 이하인 실험값을 나타낸 것이다. Fig. 4(a)에 나타난 바와 같이 fib Model Code는 $f_{2} / f_{c k}$ 값이 작을 때는 실험값보다 큰 $k_{m}$ 값이 적용되지만 $f_{2} / f_{c k}$ 값이 증가하면 실험값보다 작은 $k_{m}$ 값이 적용되는 것으로 나타났다. $f_{2} / f_{c k}$ 의 값이 0.05 이하인 경우와 0.005를 초과하는 경우를 구분하여 두 가지 수식을 적용하도록 규정된 Eurocode 2는 Fig. 4(b)에 나타난 바와 같이 $f_{2} / f_{c k}$ 값이 0.02~0.12 범위에서 KDS 설계기준과 유사한 결과를 보이지만, Fig. 4(a)에 나타난 바와 같이 $f_{2} / f_{c k}$ 값이 증가할수록 실험값보다 작은 $k_{m}$ 값이 적용되는 것으로 나타났다. Kim et al.(2014)의 제안에 따라 $k_{m}$ 값이 3.7인 KDS 설계기준은 Fig. 4(a)에 나타난 바와 같이 fib Model Code와 Eurocode 2에 비하여 실험값을 비교적 더 정확하게 예측하는 것으로 판단된다.

https://cdn.apub.kr/journalsite/sites/kibse/2024-002-01/N0510020104/images/kibse_02_01_04_F4.jpg

Fig. 4

Comparison of correction factor to confinement concrete strength design code

4. KDS 14 20 20 콘크리트구조 휨 및 압축 설계기준의 나선철근비

횡방향철근으로 구속된 콘크리트 부재에 축방향 압축력이 작용할 때는 구속되지 않은 피복 콘크리트가 먼저 파괴되고 구속된 심부콘크리트가 증가된 압축강도로 저항하는 파괴거동을 보인다. 이때 피복 콘크리트가 파괴될 때의 축압축력에서도 전체 단면적보다 감소된 심부단면적으로 심부콘크리트가 파괴되지 않고 저항성능을 유지하려면 소정의 횡방향철근으로 횡구속 되어야 한다. 이에 대하여 KDS 14 20 20 콘크리트구조 휨 및 압축 설계기준에는 나선철근비 $ρ_{s}$ 로 나타내는 나선철근 기둥의 최소 나선철근 양을 규정하고 있다. 나선철근비 $ρ_{s}$ 는 나선철근의 체적을 심부콘크리트의 체적으로 나눈 비율로 정의하여 식 (4)와 같이 구할 수 있다. 여기서, 심부콘크리트의 지름은 Fig. 5(a)와 같이 나선철근 바깥쪽 표면으로 측정한 지름 $d_{c}$ 로 나타내며, $A_{s p}$ 는 나선철근의 단면적이고 $s$ 는 나선철근의 수직간격이다.

(4)

ρ_{s} = \frac{A_{s p} π d_{c}}{π d_{c}^{2} / 4} = \frac{4 A_{s p}}{s d_{c}}

https://cdn.apub.kr/journalsite/sites/kibse/2024-002-01/N0510020104/images/kibse_02_01_04_F5.jpg

Fig. 5

Definition of core concrete and equilibrium of lateral forces

한편, Fig. 5(b)와 같이 반원으로 이루어진 자유물체도에서 횡구속 응력 $f_{2}$ 는 반원의 양단 나선철근에 작용하는 두 힘의 합과 원주응력에 의한 합력이 같으므로 식 (5)와 같이 나타낼 수 있다.

(5)

2 f_{y h} A_{s p} = f_{2} d_{c} s

식 (5)를 $A_{s p}$ 로 나타내는 식으로 정리하고 식 (4)에 대입하면 횡구속 응력 $f_{2}$ 를 식 (6)과 같이 나타낼 수 있다.

(6)

f_{2} = \frac{1}{2} ρ_{s} f_{y h}

한편, 전술한 바와 같이 피복 콘크리트가 파괴될 때의 축압축력에서도 전체 단면적보다 감소된 심부단면적으로 심부콘크리트가 파괴되지 않고 저항성능을 유지하려면, 횡구속효과로 증가된 콘크리트 압축강도와 심부콘크리트 단면적을 곱한 축압축력이 피복 콘크리트에 작용하는 축압축력과 같아야 한다. 즉, $A_{c h}$ 가 심부콘크리트의 단면적일 때 $k_{m} f_{2} A_{c h}$ 가 $0.85 f_{c h} (A_{g} - A_{c h})$ 와 같아야 한다. KDS 14 20 20 콘크리트구조 휨 및 압축 설계기준은 계수 $k_{m}$ 의 값을 3.7로 규정하고 있으므로, 3.7의 $k_{m}$ 값과 식 (6)을 적용하면 $k_{m} f_{2} A_{c h}$ 을 식 (7)로 구할 수 있다.

(7)

k_{m} f_{2} A_{c h} = 3.7 \times (\frac{ρ_{s} f_{y h}}{2}) A_{c h} = 1.85 ρ_{s} f_{y h} A_{c h}

이 값 $k_{m} f_{2} A_{c h}$ 는 $0.85 f_{c k} (A_{g} - A_{c h})$ 와 같아야 하므로 식 (8)로 나타낼 수 있으며, 이를 나선철근비 $ρ_{s}$ 로 정리하면 식 (9)의 최소 나선철근비를 구할 수 있다.

(8)

1.85 f_{y h} ρ_{s} A_{c h} = 0.85 f_{c h} (A_{g} - A_{c h})

(9)

ρ_{s} = 0.4595 (\frac{A_{g}}{A_{c h}} - 1) \frac{f_{c h}}{f_{y h}} ≒ 0.46 (\frac{A_{g}}{A_{c h}} - 1) \frac{f_{c k}}{f_{y h}}

한편 KDS 14 20 20 콘크리트구조 휨 및 압축 설계기준은 ACI 318 Code(2019)와 동일하게 식 (10)으로 최소 나선철근비를 규정하고 있는데, 이 식에서 $f_{y t}$ 는 나선철근의 설계기준 항복강도로서 $f_{y h}$ 와 같은 의미를 갖는다. 식 (10)의 계수 0.45는 Richart 등의 제안에 따라 4.1의 $k_{m}$ 값을 적용하여 구한 계수 0.425를 상향조정한 ACI Committee 318의 결정에 따른 것이다. 따라서 $k_{m}$ 값을 3.7로 규정하고 있는 KDS 14 20 20 콘크리트구조 휨 및 압축 설계기준에서 최소 나선철근비로 식 (10)을 유지한다면, 식 (9)의 계수 0.4595를 하향조정한 결과가 된다는 것을 인식할 필요가 있을 것이다.

(10)

ρ_{s} = 0.45 (\frac{A_{g}}{A_{c h}} - 1) \frac{f_{c k}}{f_{y t}}

5. 결 론

원형 횡방향철근으로 구속된 콘크리트의 압축강도 실험결과 189개를 대상으로 여러 연구자들이 제안한 산정 수식과 설계기준에서 규정하고 있는 수식의 계산결과를 비교분석한 결과는 다음과 같다.

1) Ahmad and Shah, Scott et al., Moon의 수식은 전반적으로 실험값보다 작은 값을 제공하는 경향을 보이며, Mander et al., Razvi and Saacioglu, fib Model Code의 수식은 전반적으로 실험값보다 큰 값을 제공하는 경향을 보인다.

2) fib Model Code의 수식에서는 콘크리트에 1.5, 철근에 1.15의 재료부분안전계수로 기준강도를 나눈 설계강도로 계산한 경우와 재료부분안전계수를 적용하지 않은 재료강도로 계산한 경우가 큰 차이는 보이지 않았으나, 재료부분안전계수를 적용한 경우가 더 좋은 정확성을 나타내었다.

3) Desayi et al., El-Dash and Ahmad, Sun and Sakino, Eurocode 2, 한국 KDS 설계기준의 수식은 비교적 변동성이 적었고, 변동계수가 0.132로 모든 수식 중 가장 작은 값을 보이며 평균값이 1.028이고 표준편차가 0.136인 KDS 24 14 21 콘크리트교 설계기준 및 KDS 14 20 20 콘크리트구조 휨 및 압축 설계기준의 수식이 실험값을 비교적 정확하게 예측하는 것으로 나타났다.

4) KDS 14 20 20 설계기준에 규정된 최소 나선철근비 수식의 계수 0.45는 Richart et al.의 제안에 따라 4.1의 $k_{m}$ 값을 적용하여 구한 계수 0.425를 상향조정한 ACI Committee 318의 결정에 따른 것인데, KDS 14 20 20에서 규정하고 있는 3.7의 $k_{m}$ 값을 적용하여 이론적으로 구한 최소 나선철근비 수식의 계수 0.4595를 하향조정한 결과가 된다는 것을 인식할 필요가 있을 것이다.

5) 이 연구에서의 실험자료의 재료강도는 콘크리트의 경우 20~60 MPa, 철근의 경우 300~500 MPa가 많이 분포 되어있었다. 이는 연구의 대부분이 1900년대 후반과 2000년 초반에 이루어진 것으로 그 당시에 주로 사용된 재료강도로 실험이 진행되었다. 따라서, 향후 최근에 개발된 고강도 재료를 적용한 실험자료를 추가하여 분석한다면 더 높은 신뢰성을 갖는 계산식이 개발될 수 있을 것으로 판단된다.

References

ACI Committee 318 (2019) Building Code Requirements for Structural Concrete (ACI 318-19) and Commentary. Farmington Hills, MI; American Concrete Institute (ACI).

Ahmad, S. H. and Shah, S. P. (1982) Stress-Strain Curves of Concrete Confined by Spiral Reinforcement, ACI Journal 79(64), 484-490.

10.14359/10922

Assa, B., Nishiyama, M. and Watanabe, F. (2001) New Approach for Modeling Confined Concrete. Ⅰ : Circular Columns, Journal of Structural Engineering, ASCE, 743-750.

10.1061/(ASCE)0733-9445(2001)127:7(743)

Bing, L., Park, R. and Tanaka, H. (2001) Stress-Strain Behavior of High-Strength Concrete Confined by Ultra-High and Normal Strength Transverse Reinforcement, ACI Structural Journal 395-406.

Desayi, P., Sundara Raja Iyengar, K. T. and Sanjeeva Reddy, T. (1978) Equation for Stress-Strain Curve of Concrete Confined in Circular Steel Spiral, Material and Structures 11(5), 339-345.

10.1007/BF02473875

El-Dash, K. M. and Ahmad, S. H. (1995) A Model for Stress-Strain Relationship of Spirally Confined Normal and High-Strength Concrete Columns, Magazine of Concrete Research, 47(171), 177-184.

10.1680/macr.1995.47.171.177

Eurocode 2 (2004) Design of Concrete structures, Part 1-1 General Rules and Rules for Buildings, European Committee for Standardization (Eurocode).

fib (2010) fib Model Code for Concrete Structures, The International Federation for Structural Concrete, lausanne, Switzerland (fib).

Issa, M. and ToBaa, H. (1994) Strength and ductility enhancement in high-strength confined concrete, Magazine of Concrete Research 46(168), 177-189.

10.1680/macr.1994.46.168.177

KCI (Korea Concrete Institute) (2022) Flexure and Axial Compression (KDS 14 20 20), Structural Concrete Design Code and Commentary. Seoul, Korea: KCI. (In Korean)

KIBSE (Korean Institute of Bridge and Structural Engineers) (2021) Concrete Bridge Design (Limit State Design Method) (KDS 24 14 21). Sejong, Korea: KIBSE. (In Korean)

Kim, H. Y., Choi, J. H., Hwang, D. K., Choi, H. Y., Park, K. B. and Lee, J. H. (2014) Evaluation of Confinement Effect of Circular Section concrete Confined by Transverse Reinforcement, Proceedings of the Korea Concrete Institute, 26(2), October, 237-238.

Kim, S. W., Kim, Y. S., Yun, G. J., Lee, J. Y. and Kim, K. H. (2012) Confinement Effect of High-Strength Steel Spirals According to Compressive Strength of Concrete, Journal of the Korea Institute for Structural Maintenance and Ispection 16(4), 89-98.

10.11112/jksmi.2012.16.4.089

Mander, J. B., Priestley M. J. N. and Park, R. (1988a) Theoretical Stress-Strain Model for Confined Concrete, Journal of Structural Engineering, ASCE, 1804-1825.

10.1061/(ASCE)0733-9445(1988)114:8(1804)

Mander, J. B., Priestley M. J. N. and Park, R. (1988b) Observed Stress-Strain Behavior of Confined Concrete, Journal of Structural Engineering, ASCE, 1827-1849.

10.1061/(ASCE)0733-9445(1988)114:8(1827)

Martinez-Morales, Salvador (1983) Spirally-Reinforced High-Strength Concrete Columns, A doctoral thesis, Cornell University.

Moon, C. H. (2010) A Stress-Strain Model of High-Strength Concrete Confined with High-Strength Transverse Reinforcement, a Master's thesis, SungKyunKwan University.

Razvi, Salim R. and Saatcioglu Murat (1999a) Confinement Model for High-Strength Concrete, Journal of Structural Engineering, ASCE, 281-289.

10.1061/(ASCE)0733-9445(1999)125:3(281)

Razvi, Salim R. and Saatcioglu Murat (1999b) Circular High-Strength Concrete Columns under Concentric Compression, ACI Structural Journal 817-825.

Richart, F. E., Brandtzaeg, A. and Brown, R. L. (1928) A Study of the Failure of Conrete under Combined Compressive Stress, University of Illinois.

Sakino, K. (1993) Investigation on Confined HSC Columns, Research Report of the Integrated Research (NewRC) Project submitted to Ministry of Construction of Japan.

Scott, B. D., Park, R. and Priestley, M. J. N. (1982) Stress-Strain Behavior of Concrete Confined by Overlapping Hoops at Low and High Strain Rates, ACI Journal 79(2), 13-273.

10.14359/10875

Sun, Y. P. and Sakino, K. (2000) A Compressive Stress-Strain Model for High-Strength Concrete Confined by Circular Transverse Reinforcement, Composite and Hybrid Structures: Proceeding of the Sixth ASCCS International Conference on Steel-Concrete Composite Structures, Los Angeles, Califonia, U.S.A., 1067-1074.

Yoo, H. J. (2010) A Study on Confinement Effect of High Strength Spirals, a Master's thesis, Yeungnam University.

Journal of Structure Research and Practice ISSN:3022-4241(Print) 3022-7267(Online) 한국교량및구조공학회 논문집

Preview

Evaluation of Prediction Equations for Confined Circular Concrete Members of Core Concrete Compressive Strength

ABSTRACT

MAIN

Fig. 1

Confining effect by transverse reinforcement

Table 1.

Proposed equations of confined concrete compression strength

Fig. 2

Distribution of material strength

Fig. 3

Comparison of confined concrete compressive strength and predicted values

Table 2.

Maximum, minimum, average, standard deviation and coefficient of variation of test/equation ratio

(1)

(2)

(3)

Fig. 4

Comparison of correction factor to confinement concrete strength design code

(4)

Fig. 5

Definition of core concrete and equilibrium of lateral forces

(5)

(6)

(7)

(8)

(9)

(10)

References