Remaining Fatigue Life Estimation under Various Loading Conditions using Walker Equation

Ohjun Kwon; Hoon Sohn; Hyung Jin Lim

doi:10.22725/JSRP.2024.2.2.82

Preview

Research Article

Journal of Structure Research and Practice. 31 December 2024. 82-93
https://doi.org/10.22725/JSRP.2024.2.2.82

Remaining Fatigue Life Estimation under Various Loading Conditions using Walker Equation

다양한 하중 조건에서 Walker Equation을 이용한 잔여 수명 추정

Ohjun Kwon¹

Hoon Sohn²

Hyung Jin Lim³^*

권 오준¹

손 훈²

임 형진³^*

¹Post-Doctoral Researcher, Nondestructive Metrology Group, Korea Research Institute of Standards and Science, Daejeon 34113, Korea

²Professor, Department of Civil and Environmental Engineering, KAIST, Daejeon 34141, Korea

³Professor, Department of Civil and Energy System Engineering, Kyonggi University, Suwon 16227, Korea

¹한국표준과학연구원 비파괴측정그룹 박사후연구원

²한국과학기술원 건설및환경공학과 교수

³경기대학교 사회에너지시스템공학과 교수

^{*Corresponding Author}

License (open-access, http://creativecommons.org/licenses/by-nc/4.0/):

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

In this study, the remaining fatigue life estimation technique under various uniaxial loading conditions is developed using the Walker equation. First, the Walker equation parameters are estimated from multiple specimen tests by applying constant-amplitude cyclic uniaxial loading with different stress levels. Next, the stress applied to the target structure under various uniaxial loading conditions is converted into the equivalent uniform cyclic stress with a constant stress range and mean stress. Then, the fatigue crack length and fatigue life of the target structure are estimated based on the Walker equation. Finally, the remaining fatigue life is estimated using the converted equivalent uniform cyclic stress and estimated fatigue life. The performance of the developed technique is experimentally validated using notched aluminum plate specimens under various uniaxial loading conditions.

Keywords

remaining fatigue life

walker equation

equivalent uniform cyclic stress

fatigue life

본 연구에서는 Walker equation을 이용하여 다양한 하중 조건에 적용 가능한 잔여 수명 추정 기술을 개발하였다. 먼저 24개의 알루미늄 평판 시편을 이용해 피로 실험을 수행하여 하중 사이클에 따른 피로 균열 길이를 측정하였고, 측정된 피로 균열 길이 데이터로부터 시편의 Walker equation parameters를 추정하였다. 다음으로 추정된 Walker equation parameters를 이용하여 시편에 가해진 다양한 $∆ σ$ 와 $σ^{m e a n}$ 을 가지는 하중을 하나의 $∆ σ$ 와 $σ^{m e a n}$ 을 가지는 등가 하중으로 변환하였다. 그리고 Walker equation 기반으로 추가 등가 하중에 따른 피로 균열 길이와 시편의 피로 수명을 추정하였다. 마지막으로 변환된 등가 하중과 계산된 피로 수명을 이용해서 시편의 잔여 수명을 추정하였다. 개발된 잔여 수명 추정 기술의 성능은 노치가 있는 알루미늄 평판 시편을 이용해 다양한 하중 조건에서 성공적으로 검증되었다.

키워드

잔여 수명 추정

Walker equation

등가 하중 변환

피로 수명

MAIN

1. 서 론
2. 다양한 하중 조건에서 잔여 수명 추정 기술 개발
2.1 잔여 수명 추정 기술 개요
2.2 등가 하중 변환
2.3 피로 균열 길이 및 피로 수명 추정
3. 실험 검증
3.1 Walker equation parameters 추정
3.2 유도된 하중 사이클과 하중 조건 사이의 관계식 검증
3.3 피로 균열 길이 및 피로 수명 추정 성능 검증
3.4 다양한 하중 조건에서 잔여 수명 추정
4. 결 론

1. 서 론

강구조물에 반복적인 하중이 가해져 발생한 피로 균열은 강구조물 파괴의 주요 원인으로 사용 중인 강구조물 파괴의 약 90%가 피로 균열에 의한 것으로 보고되었다(Campbell 2008). 최근 피로 균열로 인한 강구조물 파괴를 사전에 방지하기 위하여 X-ray, 열화상 카메라, 초음파 등을 이용한 다양한 피로 균열 검출 기술들이 개발되었다(Jang et al. 2023). 그러나 피로 균열을 검출하여도 강구조물의 파괴가 바로 발생하지는 않기 때문에 효과적인 강구조물의 유지 관리 및 안전성 확보를 위해서는 피로 균열이 발생했을 때 사용 가능한 잔여 수명을 추정하는 것이 중요하다.

지난 수십 년 동안 강구조물의 잔여 수명을 추정하기 위해 Paris-Erdogan equation을 이용한 기술들이 개발 되어왔다(Coppe et al. 2012). Paris-Erdogan equation은 가해진 하중 사이클과 피로 균열 길이 사이의 관계를 나타내는 방정식이며, 이 방정식을 이용하면 하중 사이클에 따른 피로 균열 길이와 잔여 수명을 추정할 수 있다. 하지만 Paris-Erdogan equation을 이용한 기술은 일정한 진폭을 가지는 하중 조건에서만 피로 균열 길이와 잔여 수명을 추정할 수 있으므로, 다양한 크기의 하중이 가해지는 강구조물에는 적용할 수 없다는 한계가 있다(Abou 2015). 최근에는 컴퓨터 하드웨어의 비약적인 발전과 기술적 난제들이 해결되면서 인공신경망을 이용한 데이터 기반의 잔여 수명 추정 기술들이 많이 개발되었다(Yang 2021). 하지만 데이터 기반의 기술들은 인공신경망을 훈련하기 위해 다양한 하중 조건에서 피로 실험을 통해 많은 양의 데이터를 획득해야 하며, 훈련에 사용되지 않은 하중이 강구조물에 가해지면 잔여 수명 추정 오차가 크게 발생한다는 한계가 있다.

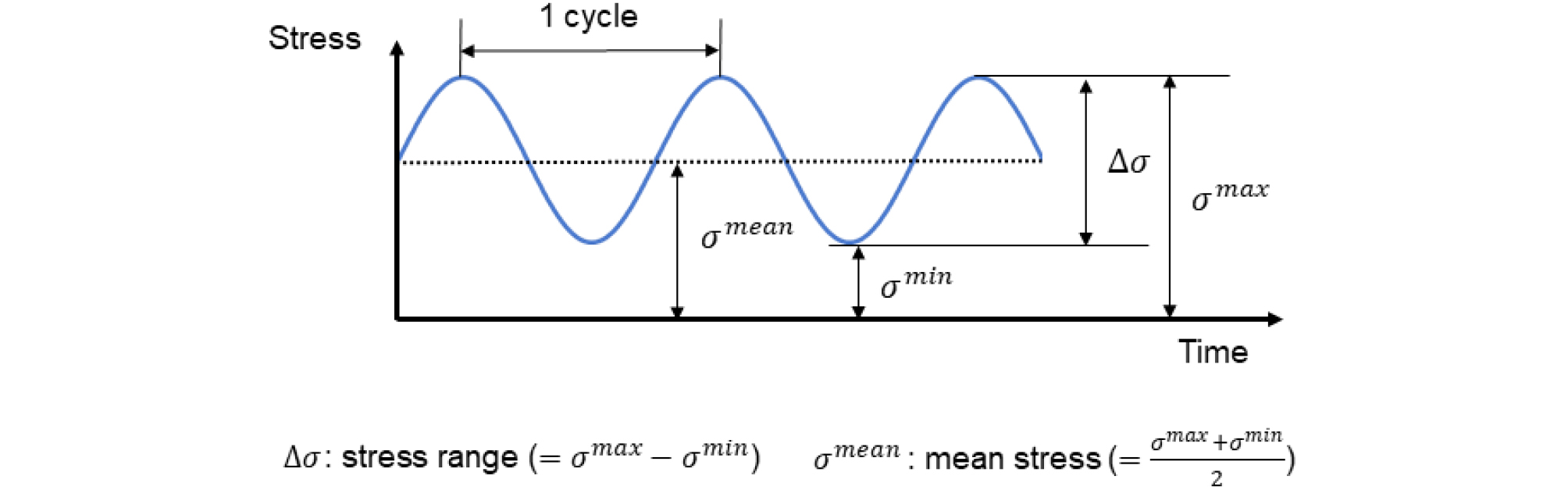
하중 사이클에 따른 피로 균열 길이와 잔여 수명은 강구조물에 가해진 하중의 응력 범위( $∆ σ$ )와 평균 응력( $σ^{m e a n}$ )에 영향을 많이 받기 때문에 다양한 하중 조건에서 잔여 수명을 정확히 추정하기 위해서는 $∆ σ$ 와 $σ^{m e a n}$ 를 동시에 고려해야만 한다(Zhu et al. 2017). Fig. 1은 강구조물에 가해진 하중의 $∆ σ$ 와 $σ^{m e a n}$ 가 무엇인지 보여준다. 본 연구에서는 Walker equation을 이용하여 다양한 하중 조건이 가해지는 강구조물에 적용할 수 있는 잔여 수명 추정 기술을 개발하였다. Walker equation은 $∆ σ$ 와 $σ^{m e a n}$ 를 동시에 고려하여 하중 사이클과 피로 균열 길이 사이의 관계를 나타낸 방정식이며, 이 방정식을 이용하면 응력 범위와 평균 응력이 다른 하중 조건에서도 잔여 수명 추정이 가능하다(Dowling et al. 2009). 먼저 Walker equation을 이용하여 하중 사이클과 하중 조건( $∆ σ$ 와 $σ^{m e a n}$ ) 사이의 관계식을 유도하였으며, 알루미늄 평판 시편을 대상으로 유도된 관계식을 실험적으로 검증하였다. 다음으로 다양한 하중 조건에서 다수의 피로 실험을 수행해 Walker equation parameters를 추정하였고, 추정된 parameters와 유도된 관계식을 이용하여 강구조물에 가해진 다양한 $∆ σ$ 와 $σ^{m e a n}$ 을 가지는 하중을 하나의 $∆ σ$ 와 $σ^{m e a n}$ 을 가지는 등가 하중으로 변환하였다. 그리고 Walker equation을 이용하여 하중 사이클에 따른 피로 균열 길이와 강구조물의 피로 수명을 계산하였다. 마지막으로 변환된 등가 하중과 계산된 피로 수명을 이용해 강구조물의 잔여 수명을 추정하였다. 노치가 있는 알루미늄 평판 시편을 대상으로 개발된 잔여 수명 추정 기술의 성능을 검증하였으며, 개발된 기술은 다양한 하중 조건에서 높은 정확도로 잔여 수명 추정이 가능함을 확인하였다.

https://cdn.apub.kr/journalsite/sites/kibse/2024-002-02/N0510020203/images/kibse_02_02_03_F1.jpg

Fig. 1

Schematic diagram of stress range and mean stress

본 논문은 다음과 같이 구성되어 있다. 2장에서는 다양한 하중 조건에서 잔여 수명을 추정하는 방법과 Walker equation을 이용한 하중 사이클과 하중 조건 사이의 관계식 유도에 관해 설명하였다. 3장에서는 노치가 있는 알루미늄 평판 시편을 대상으로 유도된 관계식의 유효성과 개발된 잔여 수명 추정 기술의 성능을 검증하였다. 마지막으로 4장에서는 논문의 간략한 요약과 논의를 다루었다.

2. 다양한 하중 조건에서 잔여 수명 추정 기술 개발

2.1 잔여 수명 추정 기술 개요

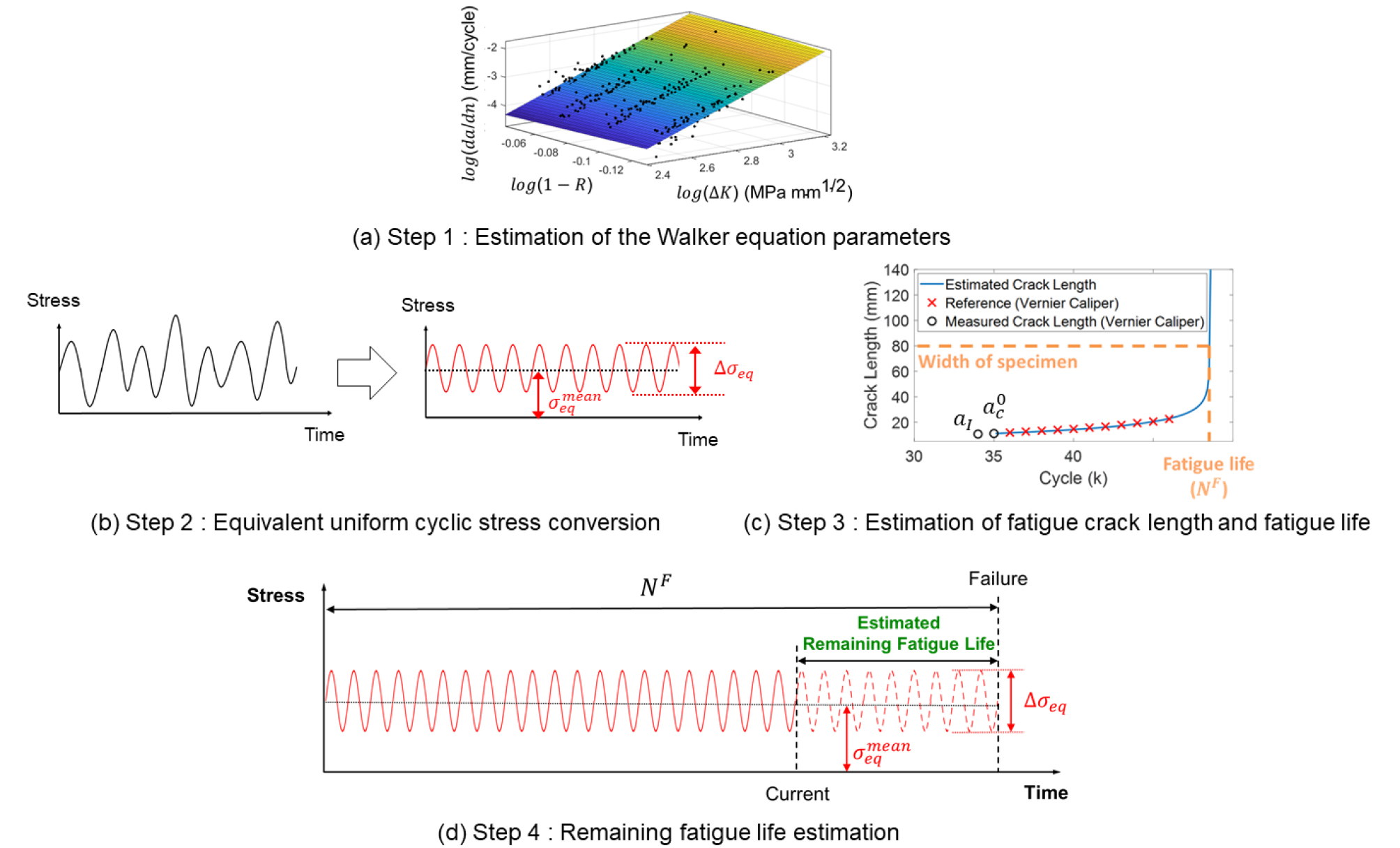
Fig. 2는 다양한 하중 조건에서 개발된 기술을 이용하여 잔여 수명을 추정하는 방법을 보여준다. 개발된 잔여 추정 기술은 총 4개의 단계로 구성되어 있으며, 각 단계에 대한 설명은 다음과 같다.

https://cdn.apub.kr/journalsite/sites/kibse/2024-002-02/N0510020203/images/kibse_02_02_03_F2.jpg

Fig. 2

Overview of developed remaining fatigue life estimation technique

1 단계 : Walker equation parameters 추정

Walker equation은 $∆ σ$ 와 $σ^{m e a n}$ 를 동시에 고려하여 하중 사이클과 피로 균열 길이 사이의 관계를 나타낸 방정식으로 다음과 같이 정의 된다(Dowling et al. 2009).

(1)

\frac{d a}{d n} = C {[\frac{∆ K}{{(1 - R)}^{1 - γ}}]}^{m}

여기서, $a$ 는 하중 사이클에 따른 피로 균열 길이, $n$ 은 강구조물에 가해진 하중 사이클 횟수, $R$ 은 하중 비, $∆ K$ 는 stress-intensity factor(SIF) 범위, $C$ , $m$ , $γ$ 은 Walker equation parameters이다. 평판 구조물에 단축 인장 하중이 가해질 때, $∆ K$ 는 다음과 같이 정의된다(Jang and Sohn 2023).

(2)

∆ K = σ S (a) \sqrt{π a}

여기서, $S (a)$ 는 균열 길이에 의해 정해지는 형성 인자이다. Eq. (1)의 $R$ 은 $∆ σ$ 와 $σ^{m e a n}$ 을 이용하여 다음과 같이 나타낼 수 있다.

(3)

R = \frac{σ^{m i n}}{σ^{m a x}} = \frac{2 σ^{m e a n} - ∆ σ}{2 σ^{m e a n} + ∆ σ}

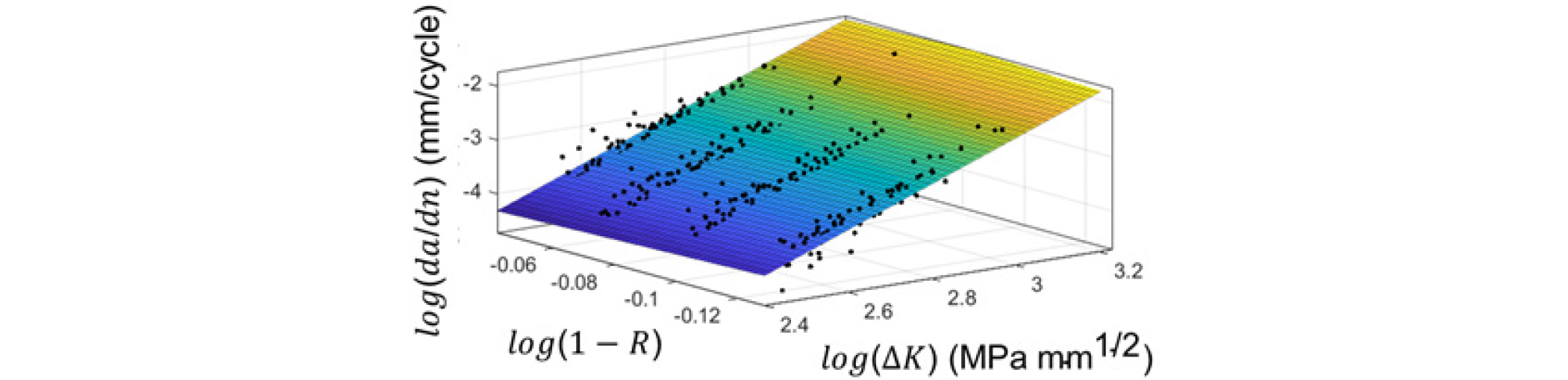
Eq. (1)의 Walker equation parameters를 추정하기 위해서는 다수의 시편을 이용하여 다양한 하중 조건에서 하중 사이클에 따른 피로 균열 길이를 측정하고, Fig. 2의 (a)와 같이 측정된 피로 균열 길이 데이터를 log-log scale로 변환한 후 선형회귀 분석을 수행해야 한다(Pandie et al. 2022).

2 단계 : 등가 하중 변환

Fig. 2의 (b)와 같이 다양한 $∆ σ$ 와 $σ^{m e a n}$ 를 가지는 하중을 1단계에서 추정한 Walker equation parameters를 이용하여 등가 응력 범위( $∆ σ_{e q}$ )와 등가 평균 응력( $σ_{e q}^{m e a n}$ )을 가지는 등가 하중으로 변환 시켜준다. Walker equation parameters를 이용한 등가 하중 변환에 대한 자세한 설명은 2.2에 제공된다.

3 단계 : 피로 균열 길이 및 피로 수명 추정

반복적인 하중으로 강구조물에 초기 균열( $a_{I}$ )이 발생하면 버니어 캘리퍼스를 이용하여 초기 균열 길이를 측정한다. 그리고 추가적인 하중이 강구조물에 가해진 후에 초기 균열에서 성장한 균열 길이( $a_{C}^{0}$ )를 버니어 캘리퍼스를 이용해 한 번 더 측정한다. 다음으로 Waler equation 기반으로 측정된 $a_{I}$ 와 $a_{C}^{0}$ 를 이용해 추가적인 하중에 따른 균열 길이를 추정한다(Fig. 2의 (c)). 또한, 추정된 피로 균열 길이가 강구조물의 폭보다 커질 때의 하중 사이클을 강구조물의 피로 수명( $N^{F}$ )으로 정의한다. 피로 균열 길이 및 피로 수명 추정에 대한 자세한 설명은 2.3에 제공된다.

4 단계 : 잔여 수명 추정

마지막으로 Fig. 2의 (d)와 같이 추정된 $N^{F}$ 와 강구조물에 가해진 변환된 등가 하중의 사이클 차이에 해당하는 잔여 수명을 계산한다.

2.2 등가 하중 변환

Eqs. (2)와 (3)을 Eq. (1)에 대입하고, Eq. (1)을 적분하면 다음과 같이 $a$ 와 $n$ 사이의 관계를 유도할 수 있다(Amura and Meo 2012).

(4)

a = {[n C {(∆ σ S (a) \sqrt{π a} {(\frac{σ^{m e a n} + ∆ σ / 2}{∆ σ})}^{1 - γ})}^{m} (1 - \frac{m}{2}) + {a_{0}}^{1 - \frac{m}{2}}]}^{{(1 - \frac{m}{2})}^{- 1}}

여기서, $a_{0}$ 는 초기 미세 균열 길이이다. Eq. (4)을 통해 피로 균열 길이가 $a$ 까지 성장하는 데 필요한 $n$ 은 강구조물에 가해지는 하중 조건( $∆ σ$ 와 $σ^{m e a n}$ )에 의해 결정되는 것을 알 수 있다. 강구조물에 가해진 하중 조건이 $∆ σ_{i}$ 와 $σ_{i}^{m e a n}$ 일 때 피로 균열이 $a$ 까지 성장하기 위한 $n$ 을 $n_{i}$ 로 정의했을 때, Eq. (4)로부터 $n_{1}$ 과 $n_{2}$ 의 비는 다음과 같이 유도된다.

(5)

\frac{n_{1}}{n_{2}} = {[(\frac{∆ σ_{2}}{∆ σ_{1}}) {(\frac{2 σ_{2}^{m e a n} + ∆ σ_{2}}{2 σ_{1}^{m e a n} + ∆ σ_{1}})}^{1 - γ}]}^{m}

Eq. (5)의 $m$ 과 $γ$ 은 2.1의 1단계에서 추정된다. Eq. (5)를 이용하면 다양한 $∆ σ_{i}$ 와 $σ_{i}^{m e a n}$ 을 가지는 하중 사이클을 다음과 같이 $∆ σ_{e q}$ 와 $σ_{e q}^{m e a n}$ 에 해당하는 하중 사이클( $n_{e q}$ )로 변환할 수 있다.

(6)

n_{e q} = n_{i} {[(\frac{∆ σ_{i}}{∆ σ_{e q}}) {(\frac{2 σ_{i}^{m e a n} + ∆ σ_{i}}{2 σ_{e q}^{m e a n} + ∆ σ_{e q}})}^{1 - γ}]}^{m}

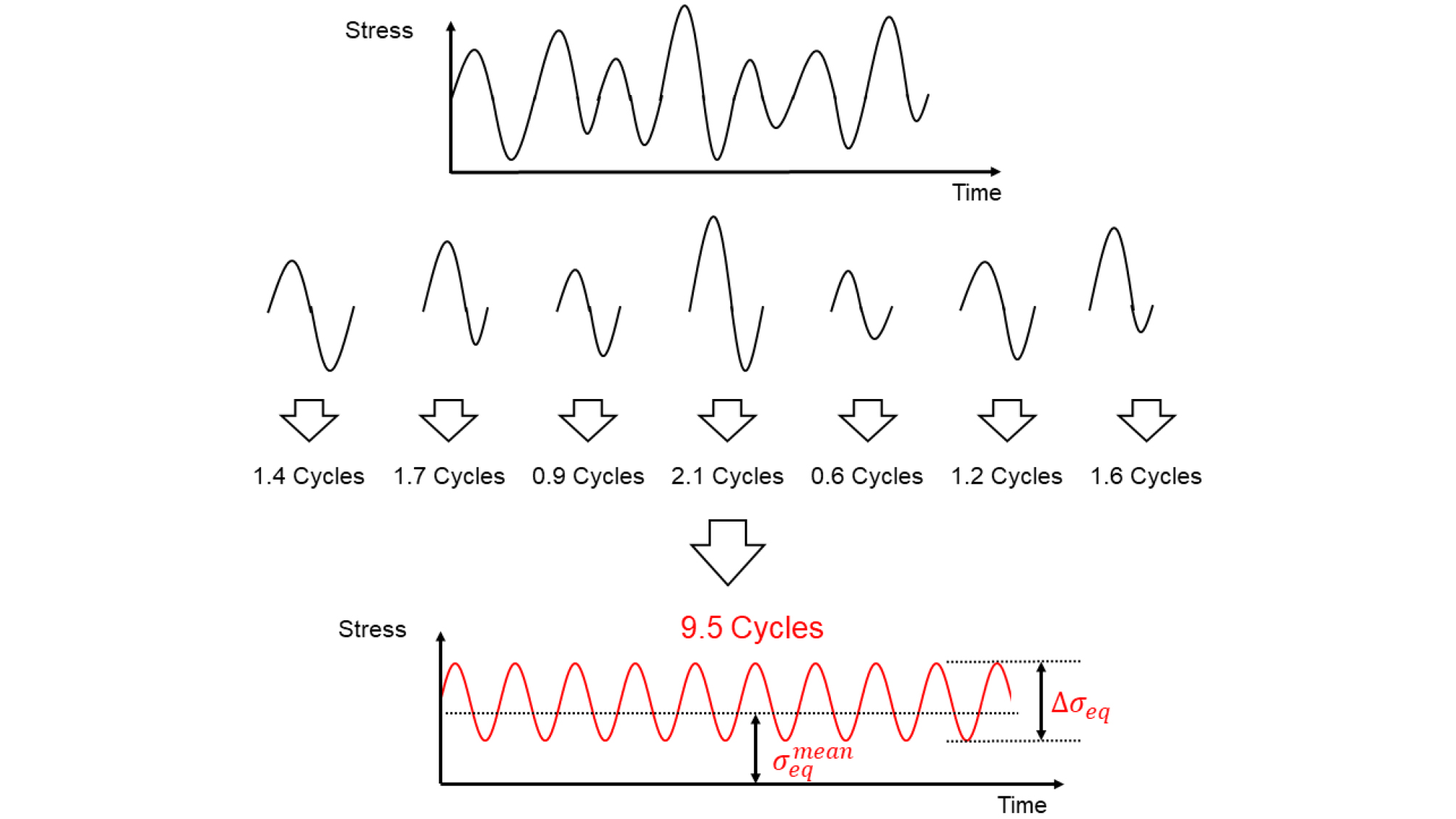
Fig. 3은 Eq. (6)를 이용해 다양한 $∆ σ$ 와 $σ^{m e a n}$ 를 가지는 하중을 $∆ σ_{e q}$ 와 $σ_{e q}^{m e a n}$ 을 가지는 등가 하중으로 변환하는 예시이다. 등가 하중으로 변환한 후에 잔여 수명을 추정함으로써 구조물의 잔여 수명을 정량적으로 평가할 수 있다.

https://cdn.apub.kr/journalsite/sites/kibse/2024-002-02/N0510020203/images/kibse_02_02_03_F3.jpg

Fig. 3

Example of equivalent uniform cyclic stress conversion

2.3 피로 균열 길이 및 피로 수명 추정

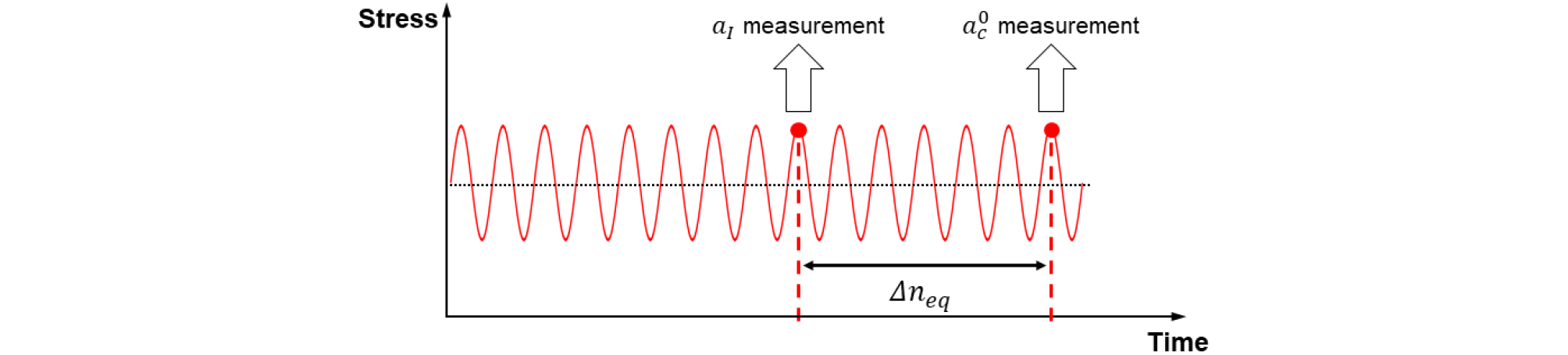
강구조물에 가해진 다양한 하중으로 인해 피로 균열이 발생했을 때, 버니어 캘리퍼스를 이용하여 발생한 피로 균열의 길이 $a_{I}$ 를 측정한다. 그리고 Fig. 4와 같이 추가적인 등가 하중( $∆ n_{e q}$ )이 강구조물에 가해진 후, $a_{I}$ 에서 성장한 균열 길이 $a_{C}^{0}$ 를 버니어 캘리퍼스를 이용하여 한 번 더 측정한다. 측정된 $a_{I}$ 와 $a_{C}^{0}$ 의 관계는 Walker equation을 이용해 다음과 같이 유도할 수 있다(Lim et al. 2019).

https://cdn.apub.kr/journalsite/sites/kibse/2024-002-02/N0510020203/images/kibse_02_02_03_F4.jpg

Fig. 4

Measurement of fatigue crack lengths ( $a_{I}$ and $a_{C}^{0}$ )

(7)

a_{C}^{0} = a_{I} + ∆ n_{e q} C {(∆ σ_{e q} S (a_{I}) \sqrt{π a_{I}} {(\frac{σ_{e q}^{m e a n} + ∆ σ_{e q} / 2}{∆ σ_{e q}})}^{1 - γ})}^{m} = a_{I} + ∆ n_{e q} A {(S (a_{I}) \sqrt{a_{I}})}^{m}

여기서, $A$ 와 $S (a_{I})$ 는 아래와 같다(Atzori et al. 2008).

(8)

A = C {(∆ σ_{e q} \sqrt{π} {(\frac{σ_{e q}^{m e a n} + ∆ σ_{e q} / 2}{∆ σ_{e q}})}^{1 - γ})}^{m}

(9)

S (a_{I}) = \sqrt{\frac{2 W}{π a_{I}} \tan \frac{π a_{I}}{2 W}} \frac{0.752 + 2.02 (a_{I} / W) + 0.37 {(1 - \sin \frac{π a_{I}}{2 W})}^{3}}{\cos \frac{π a_{I}}{2 W}}

여기서, $W$ 는 하중이 가해진 강구조물의 폭이다.

Eq. (8)의 $A$ 는 앞에서 추정된 Walker equation parameters와 측정된 $a_{I}$ 와 $a_{C}^{0}$ 를 이용해 다음과 같이 계산할 수 있다.

(10)

A = \frac{a^{0_{C}} - a_{I}}{∆ n_{e q} {(S (a_{I}) \sqrt{a_{I}})}^{m}}

Eq. (7)의 $A$ 를 계산하면, $a_{C}^{0}$ 에서 강구조물에 등가 하중이 $∆ n_{e q}$ 만큼 추가로 가해진 후에 성장한 피로 균열 길이를 다음과 같이 추정할 수 있다.

(11)

a_{C}^{j + 1} = a_{C}^{j} + A ∆ n_{e q} {(S (a_{C}^{j}) \sqrt{a_{C}^{j}})}^{m}, j = 0, 1, 2, 3, \dots

마지막으로 추정된 강구조물의 피로 균열 길이가 $W$ 보다 커질 때의 하중 사이클을 대상 강구조물의 $N^{F}$ 로 정의한다.

3. 실험 검증

3.1 Walker equation parameters 추정

Walker equation parameters를 추정하기 위하여 Fig. 5와 같이 노치가 있는 알루미늄 평판(6061-T6 알루미늄) 시편 24개를 제작하였다. 시편들의 폭과 길이는 80 mm와 360 mm로 동일하며, 두께는 다르게 제작되었다(사용된 시편의 두께 : 3, 6, 8, 13 mm). 시편의 형상과 치수는 한국 피로 시험 산업 표준(KS B ISO 12108)에 따라 제작하였다(ISO 2002).

https://cdn.apub.kr/journalsite/sites/kibse/2024-002-02/N0510020203/images/kibse_02_02_03_F5.jpg

Fig. 5

Aluminum plate specimen with a notch

24개의 알루미늄 시편에 $∆ σ$ 와 $σ^{m e a n}$ 가 다른 단축 인장 하중을 유압식 하중 기계(Instron 8801)를 이용하여 각각 가하였고, 반복 하중에 의한 피로 균열 길이를 0.01 mm 해상도를 가지는 버니어 캘리퍼스를 이용해 0.5 k 사이클마다 측정하였다. 시편에 가해진 단축 인장 하중은 Table 1에 나타냈으며, 단축 인장 하중은 10 Hz의 loading frequency로 시편에 가해졌다. 피로 균열 길이는 American Society for Testing and Materials(ASTM) 표준에 따라 시편 앞면과 뒷면에 발생한 피로 균열 길이의 평균으로 정의하였다(Lim et al. 2014). 또한, 피로 균열 성장 속도와 SIF 범위는 ASTM 표준에 명시된 secant method을 이용해 계산하였다(Standard 2002). 다양한 하중 조건에서 측정한 데이터를 log-log scale로 변환한 후 선형회귀 분석을 수행한 결과(Fig. 6), 알루미늄 평판 시편의 $m$ 와 $γ$ 은 각각 2.998과 0.3773이었다.

Table 1.

Summary of fatigue tests for Walker equation parameters estimation

Specimen	$∆ σ$ (MPa)	$σ^{m e a n}$ (MPa)	Thickness (mm)
1	51.675	31.694	13
2	51.675	35.139	13
3	51.675	39.273	13
4	51.675	43.407	13
5	56.498	34.450	13
6	56.498	37.895	13
7	56.498	42.029	13
8	56.498	46.852	13
9	60.632	37.206	13
10	60.632	41.340	13
11	60.632	45.474	13
12	60.632	52.364	13
13	65.455	39.962	6
14	65.455	44.096	6
15	65.455	48.919	6
16	65.455	54.431	6
17	67.522	41.340	8
18	67.522	45.474	8
19	67.522	50.986	8
20	67.522	56.498	8
21	75.101	45.474	3
22	75.101	50.986	3
23	75.101	56.498	3
24	75.101	62.699	3

https://cdn.apub.kr/journalsite/sites/kibse/2024-002-02/N0510020203/images/kibse_02_02_03_F6.jpg

Fig. 6

Fatigue tests results

3.2 유도된 하중 사이클과 하중 조건 사이의 관계식 검증

3.1에서 측정한 하중 사이클에 따른 피로 균열 길이 데이터를 이용해 2.2에서 유도한 Eq. (5)를 실험적으로 검증하였다. 실험적 검증은 강구조물에 가해진 $∆ σ$ 와 $σ^{m e a n}$ 에 따라 다음과 같이 3개의 Case에서 수행되었다.

Case 1 : $∆ σ$ 는 같고 $σ^{m e a n}$ 는 다른 경우

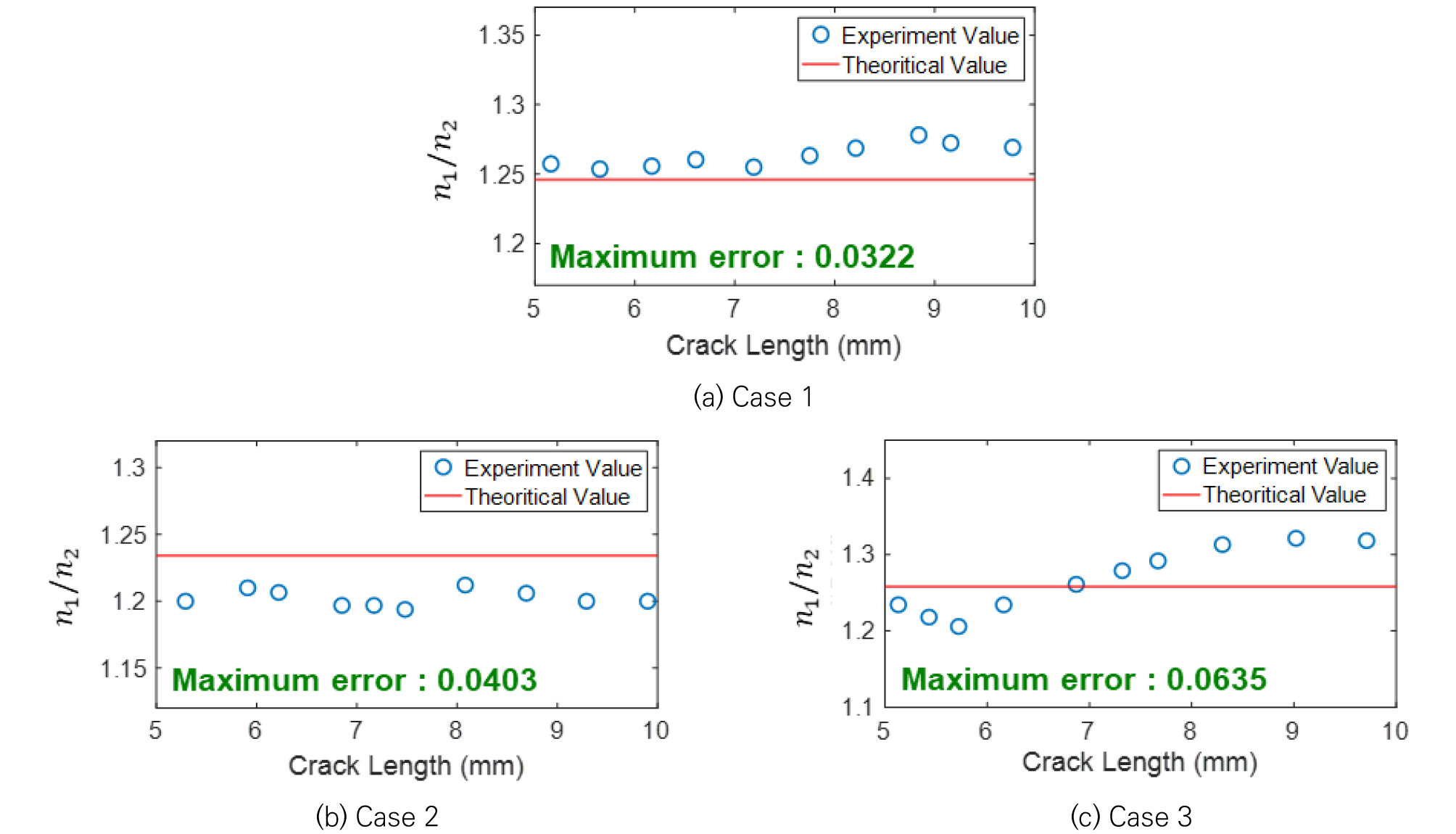
먼저 $∆ σ$ (=51.675 MPa)는 같고 $σ^{m e a n}$ ( $σ_{1}^{m e a n}$ =31.694 MPa, $σ_{2}^{m e a n}$ =37.895 MPa)는 다를 때 유도한 관계식이 유효한지 검증하였다. Eq. (5)의 이론값은 3.1에서 추정한 walker equation parameters와 알루미늄 평판 시편에 가해진 하중 조건을 이용하여 계산하였고, Eq. (5)의 실험값은 3.1에서 측정한 하중 사이클에 따른 피로 균열 길이 데이터를 이용해 계산하였다. Case 1에 대해 검증한 결과, 이론값과 실험값의 최대 오차는 0.0322로 유도한 관계식이 유효함을 확인하였다(Fig. 7(a)). 또한, 이론값이 실험값보다 항상 작았는데 이는 추정된 Walker equation의 $γ$ 값이 실제 알루미늄 평판의 $γ$ 값보다 크기 때문이다.

https://cdn.apub.kr/journalsite/sites/kibse/2024-002-02/N0510020203/images/kibse_02_02_03_F7.jpg

Fig. 7

Experimental validation results : (a) Case 1, (b) Case 2, and (c) Case 3

Case 2 : $∆ σ$ 는 다르고 $σ^{m e a n}$ 는 같은 경우

다음으로 $∆ σ$ ( $∆ σ_{1}$ =60.632 MPa, $∆ σ_{2}$ =67.522 MP)는 다르고 $σ^{m e a n}$ (=41.34 MPa)는 같을 때 유도한 관계식이 유효한지 검증하였다. Eq. (5)의 이론값과 실험값은 Case 1과 같은 방법으로 계산하였다. Case 2에 대해 검증한 결과, 이론값과 실험값의 최대 오차가 0.0403으로 Case 1과 마찬가지로 유도한 관계식이 유효함을 확인하였다(Fig. 7(b)). Case 2는 Case 1과는 반대로 추정된 Walker equation의 $γ$ 값이 실제 값보다 크게 추정되어 이론값이 항상 실험값보다 컸다.

Case 3 : $∆ σ$ 와 $σ^{m e a n}$ 가 다른 경우

마지막으로 $∆ σ$ ( $∆ σ_{1}$ =56.498 MPa, $∆ σ_{2}$ =65.455 MP)와 $σ^{m e a n}$ ( $σ_{1}^{m e a n}$ =42.029 MPa, $σ_{2}^{m e a n}$ =39.962 MPa)가 둘 다 다를 때 유도한 관계식이 유효한지 검증하였다. Eq. (5)의 이론값과 실험값은 Case 1과 같은 방법으로 계산하였다. Case 3에 대해 검증한 결과, 이론값과 실험값의 최대 오차가 0.0635로 이전 Case와 비교하여 오차가 조금 증가했지만, 여전히 이론값과 실험값 사이의 오차가 작은 것을 확인하였다(Fig. 7(c)) 따라서, 2.2에서 유도한 하중 사이클과 하중 조건 사이의 관계식은 유효하며, Eq. (6)을 이용해 다양한 $∆ σ$ 와 $σ^{m e a n}$ 를 가지는 하중을 등가 응력 범위( $∆ σ_{e q}$ )와 등가 평균 응력( $σ_{e q}^{m e a n}$ )을 가지는 등가 하중으로 변환할 수 있다.

3.3 피로 균열 길이 및 피로 수명 추정 성능 검증

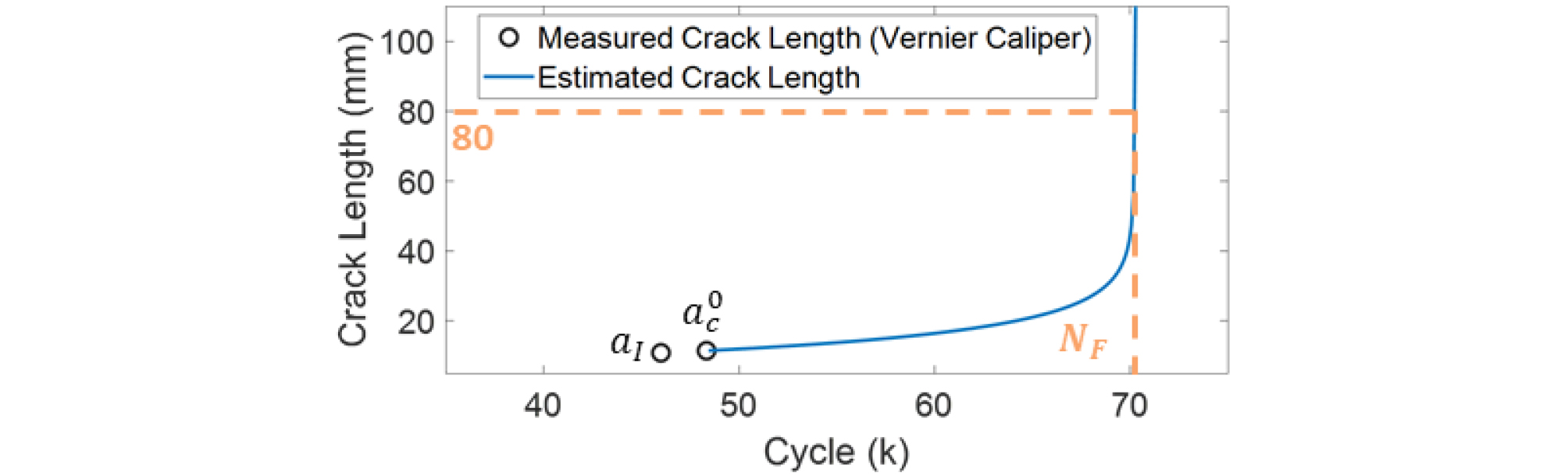
3.1에서 사용한 알루미늄 평판 시편(두께 6 mm)을 이용하여 개발된 기술의 피로 균열 길이 및 피로 수명 추정 성능을 검증하였다. 시편에 $∆ σ$ 와 $σ^{m e a n}$ 가 각각 65.455 MPa와 39.962 MPa인 단축 인장 하중을 반복해서 가하였고, 반복 하중으로 인해 발생한 $a_{I}$ 와 $a_{C}^{0}$ 를 0.01 mm 해상도를 가지는 버니어 캘리퍼스를 이용해 측정하였다. 3.1과 마찬가지로 단축 인장 하중은 10 Hz의 loading frequency로 시편에 가해졌다. $a_{I}$ 를 측정하고 시편에 1 k 사이클이 추가로 가해진 후에 $a_{C}^{0}$ 를 계측한 결과, 측정된 $a_{I}$ 와 $a_{C}^{0}$ 는 각각 10.72 mm와 11.16 mm였다.

2.3에서 설명했던 방법으로 $a_{I}$ 와 $a_{C}^{0}$ 를 이용해 피로 균열 길이 추정에 필요한 $A$ 를 계산하였고, $a_{C}^{0}$ 측정 이후 추가적인 하중으로 인한 피로 균열 길이를 Eq. (11)을 이용해 추정하였다. 계산된 $A$ 의 값은 6.577e-6이 였다. $a_{C}^{0}$ 를 측정한 이후에도 하중 사이클에 따른 피로 균열 길이의 참값 얻기 위해 시편에 단축 인장 하중을 계속 가하였고, 버니어 캘리퍼스를 이용해 피로 균열 길이를 측정하였다. Fig. 8은 Eq. (11)을 이용해 하중 사이클에 따른 피로 균열 길이를 추정한 결과를 보여준다. $a_{C}^{0}$ 측정 이후 11번의 피로 균열 길이를 추정한 결과, 최대 오차가 0.7095 mm로 높은 정확도로 피로 균열 길이를 추정할 수 있음을 확인하였다. 다음으로 추정된 피로 균열 길이를 이용해 시편의 피로 수명을 계산하였다. 추정된 피로 균열 길이가 시편의 폭인 80 mm보다 커질 때의 하중 사이클을 피로 수명으로 계산한 결과, 피로 수명 추정 오차가 -1.5 k 사이클(추정된 피로 수명 : 48.5 k, 실제 피로 수명 : 47 k, 상대 오차 : 3.19 %)로 높은 정확도로 피로 수명 추정이 가능함을 확인하였다.

https://cdn.apub.kr/journalsite/sites/kibse/2024-002-02/N0510020203/images/kibse_02_02_03_F9.jpg

Fig. 8

Experimental validation results of fatigue crack length and fatigue life estimation

3.4 다양한 하중 조건에서 잔여 수명 추정

3.1에서 사용한 알루미늄 평판 시편(두께 6 mm)을 이용해 개발된 잔여 수명 추정 기술의 성능을 검증하였다. 시편에 하중 조건이 다른 9개의 단축 인장 하중을 5 k 사이클씩 순서대로 가하였고, 다양한 하중으로 인해 시편에 발생한 $a_{I}$ 와 $a_{C}^{0}$ 를 측정하였다. 시편에 가해진 단축 인장 하중은 Table 2에 나타냈다. 단축 인장 하중은 10 Hz의 loading frequency로 시편에 가해졌다.

Table 2.

Summary of applied uniaxial cyclic loading levels for experimental validation

Number	$∆ σ$ (MPa)	$σ^{m e a n}$ (MPa)
1	62.01	48.23
2	62.01	41.34
3	62.01	34.45
4	55.12	48.23
5	55.12	41.34
6	55.12	34.45
7	48.23	48.23
8	48.23	41.34
9	48.23	34.45

$a_{I}$ 를 측정할 때 시편에 가해진 하중들의 최대 $∆ σ$ 와 최소 $∆ σ$ 들을 평균하고 빼주어 $∆ σ_{e q}$ 을 계산하였고, 가해진 $σ$ 의 평균값을 $σ_{e q}^{m e a n}$ 으로 사용했다. 계산된 $∆ σ_{e q}$ 와 $σ_{e q}^{m e a n}$ 는 각각 56.154 MPa와 38.033 MPa이 였다. 다음으로 시편에 가해진 다양한 하중들을 3.1에서 추정된 Walker equation parameters와 Eq. (6)을 이용해 $∆ σ_{e q}$ 와 $σ_{e q}^{m e a n}$ 를 가지는 등가 하중으로 변환하였다. 버니어 캘리퍼스를 이용해 $a_{I}$ 를 측정하고 시편에 3.5 k 등가 하중 사이클을 추가로 시편에 가한 후 $a_{C}^{0}$ 를 측정한 결과, 측정된 $a_{I}$ 와 $a_{C}^{0}$ 는 각각 10.87 mm와 11.47 mm였다. 2.3에서 설명했던 방법으로 $a_{I}$ 와 $a_{C}^{0}$ 를 이용해 피로 균열 길이 추정에 필요한 $A$ 를 계산하였고, $a_{C}^{0}$ 측정 이후 추가적인 하중 사이클로 인한 피로 균열 길이와 시편의 피로 수명을 추정하였다. Fig. 9는 피로 균열 길이와 피로 수명 추정 결과를 보여준다. 추정된 $N^{F}$ 와 시편에 가해진 변환된 등가 하중을 이용하여 $a_{C}^{0}$ 를 측정할 때 시편의 잔여 수명을 추정한 결과, 오차는 –3.2 k 사이클(추정된 잔여 수명 : 16.3 k, 실제 피로 수명 : 13.1 k, 상대 오차 : 24.43 %)로 높은 정확도로 잔여 수명을 추정하였다. 검증 실험 결과는 개발된 기술이 다양한 하중 조건에서 잔여 수명 추정이 가능함을 보여준다.

Fig. 9

Estimation results of fatigue crack length and fatigue life

4. 결 론

본 연구에서는 효율적인 강구조물 유지 관리를 위하여 Walker equation을 이용해 다양한 하중 조건에 적용할 수 있는 잔여 수명 추정 기술을 개발하였고, 노치가 있는 알루미늄 평판 시편을 대상으로 성능을 검증하였다. 먼저 24개의 알루미늄 평판 시편에 조건이 다른 하중들을 각각 가하였고, 하중 사이클에 따른 피로 균열 길이를 측정하였다. 그리고 측정된 데이터들을 log-log scale로 변환한 후 선형회귀 분석을 수행하여 Walker equation parameters를 추정하였다. 다음으로 추정된 Walker equation parameters를 이용해 시편에 가해진 다양한 $∆ σ$ 와 $σ^{m e a n}$ 을 가지는 하중을 하나의 $∆ σ$ 와 $σ^{m e a n}$ 을 가지는 등가 하중으로 변환하였다. 그리고 시편에 가해진 반복적인 등가 하중으로 인한 피로 균열 길이를 두 번 계측하였고, Walker equation을 기반으로 측정된 피로 균열 길이를 이용해 추가적인 등가 하중 사이클에 따른 피로 균열 길이와 시편의 피로 수명을 추정하였다. 마지막으로 변환된 등가 하중과 계산된 피로 수명을 이용해 시편의 잔여 수명을 추정하였다. 노치가 있는 알루미늄 시편을 대상으로 개발된 기술의 성능을 검증한 결과, 4 k 사이클 이내의 정확도로 잔여 수명을 추정할 수 있음을 확인하였다. 개발된 기술은 다음과 같은 uniqueness를 가진다 : (1) Walker equation을 이용한 하중 사이클과 하중 조건 사이의 관계식 유도 및 실험적 검증 수행, (2) 다양한 $∆ σ$ 와 $σ^{m e a n}$ 을 가지는 하중을 하나의 $∆ σ$ 와 $σ^{m e a n}$ 을 가지는 등가 하중으로 변환, (3) Walker equation 기반 피로 균열 길이 및 강구조물 피로 수명 추정, (4) 다양한 하중 조건에서 노치가 있는 알루미늄 평판을 대상으로 개발된 기술의 성능 검증 수행.

본 연구에서는 다양한 하중 조건에 적용할 수 있는 잔여 수명 추정 기술을 개발하였고, 실험적으로 성능을 검증하였다. 향후 연구에서는 실제 강구조물에 적용하기 위하여 loading frequency가 고정된 단축 인장 하중이 아닌 loading frequency가 고정되지 않은 랜덤 하중에도 적용할 수 있는 연구가 필요하다. 또한, 온도, 습도, 부식 등과 같은 영향을 검토할 필요가 있다.

Acknowledgements

본 연구는 국토교통부의 U-City 석·박사과정 지원사업으로 지원을 받아 수행된 연구입니다.

References

Campbell, F. C. (2008) Elements of metallurgy and engineering alloys. ASM International.

10.31399/asm.tb.emea.9781627082518

Jang, J., Liu, P., Kwon, O., Choi, J., Ma, Z. and Sohn, H. (2023) Reference-free Fatigue Crack Detection Using Deep Long Short-term Memory Network (DLSTM) and Nonlinear Ultrasonic Modulation. NDT & E International 137, 102828.

10.1016/j.ndteint.2023.102828

Coppe, A., Pais, M. J., Haftka, R. T. and Kim, N. H. (2012) Using a Simple Crack Growth Model in Predicting Remaining Useful Life. Journal of Aircraft 49(6), 1965-1973.

10.2514/1.C031808

Abou Jaoude, A. (2015) Analytic and Linear Prognostic Model for a Vehicle Suspension System Subject to Fatigue. Systems Science & Control Engineering 3(1), 81-98.

10.1080/21642583.2014.987359

Yang, J., Kang, G., Liu, Y. and Kan, Q. (2021) A Novel Method of Multiaxial Fatigue Life Prediction Based on Deep Learning. International Journal of Fatigue 151, 106356.

10.1016/j.ijfatigue.2021.106356

Zhu, S. P., Lei, Q., Huang, H. Z., Yang, Y. J. and Peng, W. (2017) Mean Stress Effect Correction in Strain Energy-based Fatigue Life Prediction of Metals. International Journal of Damage Mechanics 26(8), 1219-1241.

10.1177/1056789516651920

Dowling, N. E., Calhoun, C. A. and Arcari, A. (2009) Mean Stress Effects in Stress‐life Fatigue and the Walker Equation. Fatigue & Fracture of Engineering Materials & Structures 32(3), 163-179.

10.1111/j.1460-2695.2008.01322.x

Jang, J. and Sohn, H. (2023) Online Remaining Fatigue Life Estimation of Curved Steel Connection Using Nonlinear Ultrasonic Modulation. International Journal of Fatigue 170, 107566.

10.1016/j.ijfatigue.2023.107566

Pandie, A., Yudiana, A. R. and Hermansah, H. (2022) Fatigue and Damage Tolerance, Prediction of Crack Propagation on Plate Using Paris Equation and Walker Equation. In Proceedings of the First Multidiscipline International Conference MIC 2021, October 30 2021. Jakarta, Indonesia.

10.4108/eai.30-10-2021.2315783PMC9946164

Amura, M. and Meo, M. (2012) Prediction of Residual Fatigue Life Using Nonlinear Ultrasound. Smart materials and structures 21(4), 045001.

10.1088/0964-1726/21/4/045001

Lim, H. J., Lee, Y. J. and Sohn, H. (2019) Continuous Fatigue Crack Length Estimation for Aluminum 6061-T6 Plates with a Notch. Mechanical Systems and Signal Processing 120, 356-364.

10.1016/j.ymssp.2018.10.018

Atzori, B., Lazzarin, P. and Meneghetti, G. (2008) Fatigue Strength Assessment of Welded Joints: From the Integration of Paris' Law to a Synthesis Based on the Notch Stress Intensity Factors of the Uncracked Geometries. Engineering Fracture Mechanics 75(3-4), 364-378.

10.1016/j.engfracmech.2007.03.029

International Organization for Standardization. (2002) Metallic Materials: Fatigue Testing: Fatigue Crack Growth Method. ISO 12108. ISO.

Lim, H. J., Sohn, H., DeSimio, M. P. and Brown, K. (2014) Reference-free Fatigue Crack Detection Using Nonlinear Ultrasonic Modulation Under Various Temperature and Loading Conditions. Mechanical Systems and Signal Processing 45(2), 468-478.

10.1016/j.ymssp.2013.12.001

Standard, A. S. T. M. (2002) Standard test method for measurement of fatigue crack growth rates. (No Title), 3.

Journal of Structure Research and Practice ISSN:3022-4241(Print) 3022-7267(Online) 한국교량및구조공학회 논문집

Preview

Remaining Fatigue Life Estimation under Various Loading Conditions using Walker Equation

ABSTRACT

MAIN

Fig. 1

Schematic diagram of stress range and mean stress

Fig. 2

Overview of developed remaining fatigue life estimation technique

(1)

(2)

(3)

(4)

(5)

(6)

Fig. 3

Example of equivalent uniform cyclic stress conversion

Fig. 4

Measurement of fatigue crack lengths (aI and aC0)

(7)

(8)

(9)

(10)

(11)

Fig. 5

Aluminum plate specimen with a notch

Table 1.

Summary of fatigue tests for Walker equation parameters estimation

Fig. 6

Fatigue tests results

Fig. 7

Experimental validation results : (a) Case 1, (b) Case 2, and (c) Case 3

Fig. 8

Experimental validation results of fatigue crack length and fatigue life estimation

Table 2.

Summary of applied uniaxial cyclic loading levels for experimental validation

Fig. 9

Estimation results of fatigue crack length and fatigue life

Acknowledgements

References

Measurement of fatigue crack lengths ( $a_{I}$ and $a_{C}^{0}$ )